Levenshtein Distance Problem

The Levenshtein Distance problem, also known as the edit distance problem, is to find the lowest cost path to turn one string to another string. It is commonly used in spell checking, Google search results for ‘did you mean…’, and DNA sequencing (Bioinformatics).

An easy example is if you misspelled “word” for “wird”, there would need to be one replacement to get from “wird” to “word” (change the letter “i” to “o”). There is one algorithm that answers this problem efficiently, as we now of right now. This algorithm compares one letter of the first string to all of the characters to the other strings and gives it a ranking or a score. There are three ways you can modify a character, by inserting another character, deleting, or replacing that character. Each of these modifications cost one value.

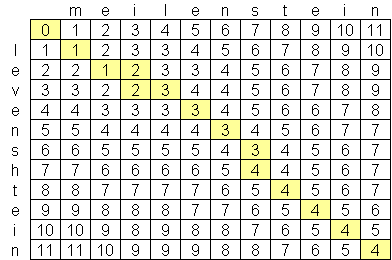
Typically, you will see this as a matrix, as shown above. The first row and first column show the length of the strings. The rest of the matrix is filled out following that you do a nested for loop, taking one letter at a time for the first string and go through the rest of the letters in the second string. Here’s a quick look with Ruby:

(1..second.length).each do |i|
  (1..first.length).each do |j|
    # Do your logic here
  end
end

We traverse this matrix starting at [1] [1] (one square diagonal of the top left square), and move to our right until we get to the end of the matrix. Then we continue to the next row and go back to 1 (matrix [2] [1]). We place a conditional in our code. If the letters we are comparing are the same, then there is no cost penalty and we take the same value as the diagonal on the square’s top left. However, if it is different, we take the minimum cost to each of our modification choices.

• Insertion: When we insert a letter in our first string, that shifts our word column, so we take the same value as to the square to its top, plus 1 for an additional modification cost.
• Deletion: Same as insertion, but we take the value of the square to its left
• Replace: We take the value of the upper left to the square and add 1 to it.

The result is at the bottom right corner, which will tell you the minimum cost of changing one string to another. If the score threshold is low enough, Google will ask you, “did you mean…” if the search ran through the algorithm and could match a more common search term.

A side note

My coding club looked at this algorithm with no prior knowledge of this problem and tried to understand it. Now that I’ve taken the time to review this, I have a much deeper understanding of this now.

Resources

Levenshtein distance implementation in different programming languages

MIT course on Algorithms: Levenshtein distance problem explained with dynamic programming